Compiler
This project is probably my 4th or 5th attempt at writing a compiler. Each attempt has gotten further and further until the snowball of uneducated decisions made it too difficult to continue, but at this point I feel very comfortable with parsing and typechecking, now I’m beginning to experiment with intermediate representations and lowering to machine-/bytecode.
Source: https://github.com/JoshuaManton/lang
Demo: https://github.com/JoshuaManton/lang/blob/master/demo.lang
This is a living document that will be added to as development continues and I decide something is interesting enough to write about.
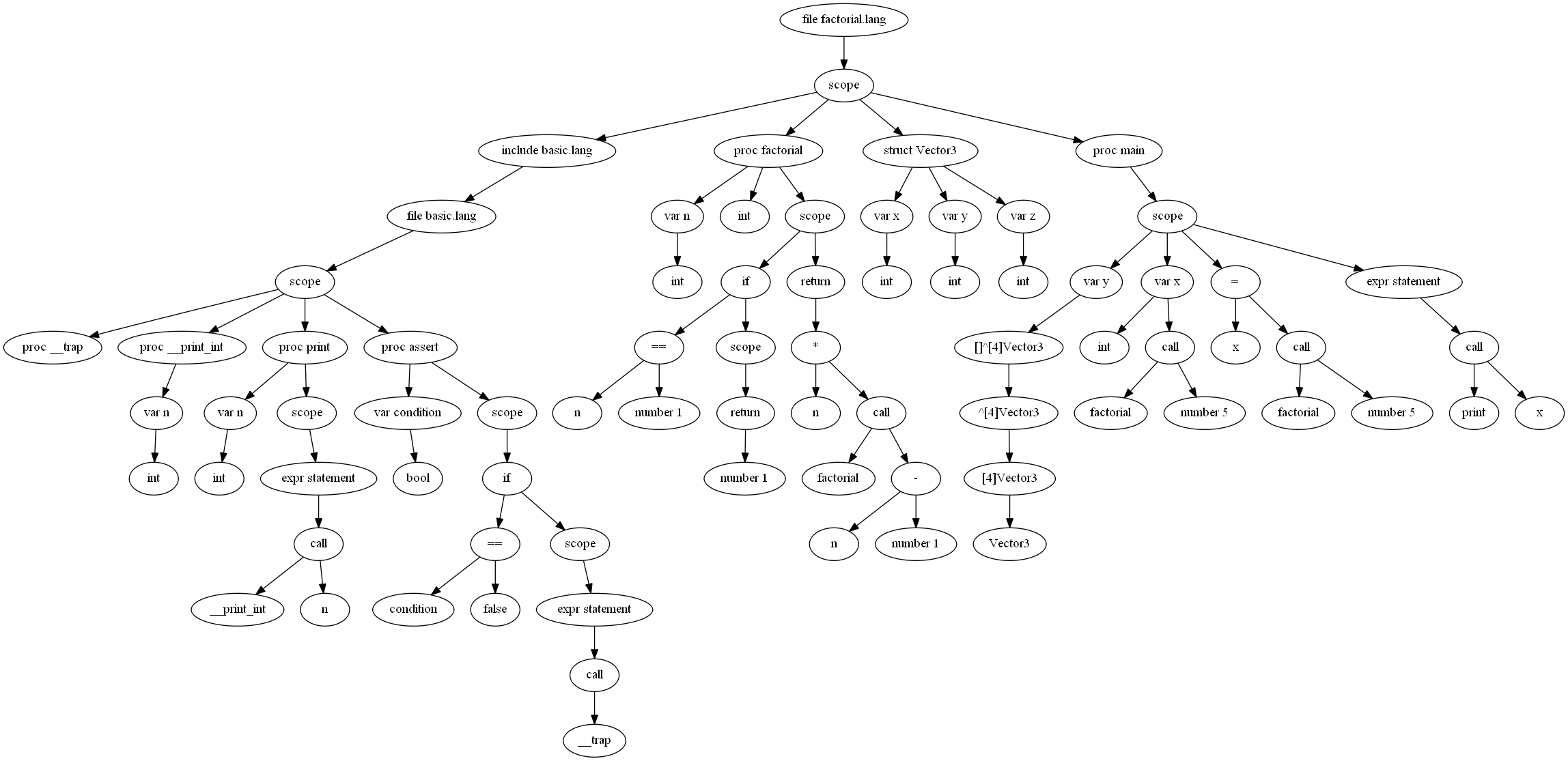
This post will give a high-level overview of the the various stages of the compiler as it currently exists, using the classic factorial program as an example.
This compiler implements a recursive-descent parser to parse source code into a syntax tree, typechecks the syntax tree and enforces the semantic rules of the language, generates an intermediate representation of the instruction stream, translates this intermediate representation to bytecode, and executes the bytecode in a virtual machine.
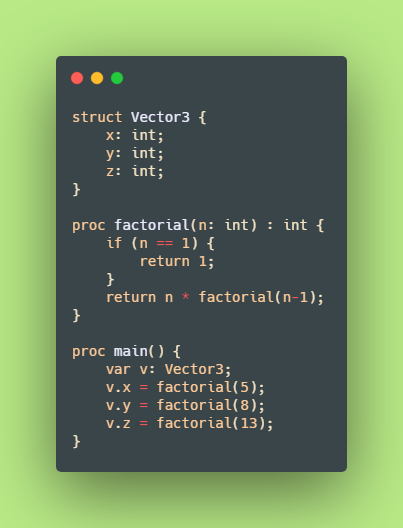
Take the following program:
#include "basic.lang" // contains VM intrinsics for print() and assert()
proc factorial(n: int) : int {
if (n == 1) {
return 1;
}
return n * factorial(n-1);
}
proc main() {
var x: int = factorial(5); // the `int` is optional, as the type can be inferred based on the return type of `factorial()`
print(x);
assert(x == 120);
}
The output of the program is, of course:
120
Parsing this code generates a syntax tree for the program (click to open full size):
Once the code is in this format the compiler can traverse the tree and do typechecking, constant evaluation, and enforce the rules of the language. For example we would immediately know that the number literal in the above program 5 is an int, so if factorial() took an f32 or a string as its parameter, that would be a compile error. At the end of the typechecking phase all types of all variables and expressions are known and the program is known to be a valid program that obeys the rules of the language.
The next step is to do another tree traversal and generate an intermediate representation (IR) of the program that is slightly closer to the final output executable code. The IR stage reasons about registers, storage of variables/values, and high-level instructions. The reason for having this representation is to do work that is common to all/most backends such as much of the work involved in register allocation, computing stack frame sizes for procedures (including the offsets of local variables), and certain high-level optimizations.
After the IR is generated it is translated to executable instructions for the actual compile target. In my case the compile target is bytecode for a virtual machine that runs within the compiler:
// contents of basic.lang omitted, it just contains some intrinsics for the VM.
factorial:
; save caller frame and return address
push rfp
push ra
; setup stack frame
mov rfp rsp
addi rsp rsp -4
; body
; IR_Load
addi rt rfp -4
load32 r1 rt
; IR_Move_Immediate
movi r2 1
; IR_Binop
eq r3 r1 r2
; IR_If
gotoifz r3 if_57
; IR_Move_Immediate
movi r3 1
; IR_Return
; return
addi rsp rsp 4
pop ra
pop rfp
push r3
mov rip ra
if_57:
; IR_Load
addi rt rfp -4
load32 r3 rt
; IR_Call
push r3
; IR_Load
addi rt rfp -4
load32 r1 rt
; IR_Move_Immediate
movi r2 1
; IR_Binop
sub r4 r1 r2
addi rt rsp -20
store32 rt r4
jump factorial
pop r4
pop r3
; IR_Binop
mul r1 r3 r4
; IR_Return
; return
addi rsp rsp 4
pop ra
pop rfp
push r1
mov rip ra
; return
addi rsp rsp 4
pop ra
pop rfp
mov rip ra
main:
; save caller frame and return address
push rfp
push ra
; setup stack frame
mov rfp rsp
addi rsp rsp -4
; body
; IR_Call
; IR_Move_Immediate
movi r1 5
addi rt rsp -20
store32 rt r1
jump factorial
pop r1
; IR_Store
addi rt rfp -4
store32 rt r1
; IR_Call
; IR_Load
addi rt rfp -4
load32 r1 rt
addi rt rsp -20
store32 rt r1
jump print
; special sauce for main()
addi rsp rsp 4
exit
As mentioned before, the above code is executed in a virtual machine that implements an ISA I made up. The VM is a pretty simple register-based VM. The compiler builds a linear list of instructions and the VM is basically just a huge switch-statement that does different work based on what the instruction is.
The full source of the VM is available here but I will walk through some of the key points of it here.
The VM struct looks like this:
VM :: struct {
registers: [Register]u64,
instructions: [dynamic]Instruction,
memory: []byte,
// some fields omitted
}
Pretty much to be expected. An array of instructions, an array of registers, and an array of bytes for memory. The instructions should probably live inside the memory array since that’s how computers actually work; will do that soon.
Register is an enum that holds each of the named registers for the VM:
Register :: enum {
rsp, rfp, rip, ra, rt, rz,
r1, r2, r3, r4,
r5, r6, r7, r8
}
Registers r1 through r8 are for users to do their normal work with; load values in, do some math, store values back to main memory. There are also some special named registers:
rspholds the address of the current stack pointer.pushing andpoping values decrements and increments the stack pointer (stack grows downwards).rfpholds the address of the current frame pointer for a procedure’s stack frame.ripholds the index of the current instruction being executed.rahold the return address of the calling procedure.rtis a utility register just for holding temporary values.rzis hard-wired to0. Writing to it does nothing and reading it gives0.
The Instruction struct is just a tagged union of all the instruction types:
Instruction :: union {
LOAD8,
LOAD16,
LOAD32,
LOAD64,
STORE8,
STORE16,
STORE32,
STORE64,
PUSH,
POP,
MOV,
MOVI,
ADD,
ADDI,
FADD,
FADDI,
// ...
}
There are of course many more instructions for doing comparisons, jumps, and math. Each instruction has its own struct holding it’s parameters:
LOAD8 :: struct { dst, p1: Register, }
LOAD16 :: struct { dst, p1: Register, }
LOAD32 :: struct { dst, p1: Register, }
LOAD64 :: struct { dst, p1: Register, }
STORE8 :: struct { dst, p1: Register, }
STORE16 :: struct { dst, p1: Register, }
STORE32 :: struct { dst, p1: Register, }
STORE64 :: struct { dst, p1: Register, }
PUSH :: struct { p1: Register }
POP :: struct { dst: Register }
MOV :: struct {
dst, src: Register,
}
MOVI :: struct {
dst: Register,
imm: i64,
}
ADD :: struct {
dst, p1, p2: Register,
}
ADDI :: struct {
dst, p1: Register,
imm: i64,
}
FADD :: struct {
dst, p1, p2: Register,
}
FADDI :: struct {
dst, p1: Register,
imm: f64,
}
// ...
As mentioned before, the VM execution is a huge switch-statement:
instruction_loop: for vm.registers[.rip] < cast(u64)len(vm.instructions) {
switch kind in vm.instructions[vm.registers[.rip]] {
case LOAD8: vm.registers[kind.dst] = cast(u64)(cast(^u8 )&vm.memory[vm.registers[kind.p1]])^;
case LOAD16: vm.registers[kind.dst] = cast(u64)(cast(^u16)&vm.memory[vm.registers[kind.p1]])^;
case LOAD32: vm.registers[kind.dst] = cast(u64)(cast(^u32)&vm.memory[vm.registers[kind.p1]])^;
case LOAD64: vm.registers[kind.dst] = cast(u64)(cast(^u64)&vm.memory[vm.registers[kind.p1]])^;
case STORE8: (cast(^u8 )&vm.memory[vm.registers[kind.dst]])^ = cast(u8 )vm.registers[kind.p1];
case STORE16: (cast(^u16)&vm.memory[vm.registers[kind.dst]])^ = cast(u16)vm.registers[kind.p1];
case STORE32: (cast(^u32)&vm.memory[vm.registers[kind.dst]])^ = cast(u32)vm.registers[kind.p1];
case STORE64: (cast(^u64)&vm.memory[vm.registers[kind.dst]])^ = cast(u64)vm.registers[kind.p1];
case PUSH: vm.registers[.rsp] -= 8; (cast(^u64)&vm.memory[vm.registers[.rsp]])^ = vm.registers[kind.p1];
case POP: vm.registers[kind.dst] = (cast(^u64)&vm.memory[vm.registers[.rsp]])^; mem.zero(&vm.memory[vm.registers[.rsp]], 8); vm.registers[.rsp] += 8;
case MOV: vm.registers[kind.dst] = vm.registers[kind.src];
case MOVI: vm.registers[kind.dst] = transmute(u64)kind.imm;
case ADD: vm.registers[kind.dst] = vm.registers[kind.p1] + vm.registers[kind.p2];
case ADDI: vm.registers[kind.dst] = vm.registers[kind.p1] + transmute(u64)kind.imm;
case FADD: vm.registers[kind.dst] = transmute(u64)(transmute(f64)vm.registers[kind.p1] + transmute(f64)vm.registers[kind.p2]);
case FADDI: vm.registers[kind.dst] = transmute(u64)(transmute(f64)vm.registers[kind.p1] + kind.imm);
case EXIT: break instruction_loop;
// ...
}
vm.registers[.rip] += 1;
vm.registers[.rz] = 0;
}
While I would like to write a “real” machine-code backend at some point, either use LLVM or generate x64 by hand, having this VM lets us do some cool things, like the following:
const TWENTY_FOUR: int = #run factorial(4);
TWENTY_FOUR is able to be constant because a #run directive will be run at compile-time, not runtime. We can evaluate factorial(4) as though it was a normal constant expression which means that in the actual executable factorial() will not be run, TWENTY_FOUR will simply be equal to 24. But this can be used to do arbitrary things like generate code, or configure the building of your program in the language itself rather than having a separate .bat file. You could run tests. You could open a socket and communicate with your build server, or get the hash of the current commit in version control and embed that in the build, all in the language itself. I have not yet implemented #run but all the pieces are in place.